Не е нова идеята да се предава информация по възможно най-икономичен начин. Например естествените говорими езици и писмени азбуки неизменно страдат от излишество. При тях обаче икономичното предаване на информация не е най-важната страна; макар и не оптимални от тази гледна точка те са удобни за използване от човек. За оптимално кодиране са разработени специални съкратени системи, каквито са например стенографската, морзовата азбука, азбуката за глухи, които са лишени от доста удобства. С навлизането на компютрите се появява възможност автоматично сравнително бързо да се "превежда" даден поток от информация на по-икономична азбука и обратно. Бързо намират приложение алгоритмите за компресиране на информация, а те от своя страна се доразработват и оптимизират, за да навлязат във всекидневна употреба. Всеки е използвал поне една универсална програма за компресиране (ARJ, ZIP, RAR, ACE) и се е възползвал от компресии на мултимедия - звук (MP3, OGG), картина (GIF, JPEG), филмов клип (MPEG), дори и извън всекидневната работа с компютрите (компресия на звук по GSM). Алгоритмите за компресия имат стабилна математическа основа и стават все по-сложни и с по-добра степен на компресия с нуждата от тяхното прилагане.
Алгоритъмът на Хъфман, разгледан тук е сравнително прост универсален алгоритъм за компресия без загуба на данни (за разлика от алгоритмите със загуба, стоящи в основата на MP3, например). При него се предполага, че имаме краен поток от числа в някакъв предварително фиксиран интервал. Ние тук ще считаме, че става дума за символи, кодирани със ASCII код, т.е. ще разглеждаме информацията като поредица от байтове (числа в интервала 0..255). Алгоритъмът се базира на простата идея, че най-често срещаните символи в поредицата трябва да се записват с най-малък брой битове. Така той построява нова азбука, която следва тази идея и след това превежда информацията в новата азбука. Кодирането е обратимо, т.е. по кодираната последователност можем да декомпресираме - да намерим първоначалната поредица.
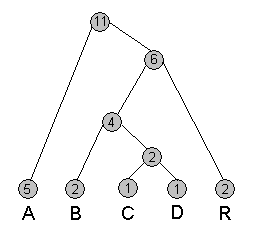
Ще считаме, че желаем да компресираме даден низ от символи. Искаме да построим двоично дърво, от което ще определим азбука за компресиране.
Алгоритъмът за построяване на дърво се състои от следните стъпки:
Така построено дървото е двоично и има точно n на брой листа, като на всяко листо отговаря един символ от честотната таблица. По начина на построение се вижда, че по-често срещаните символи се намират по-близо до корена от по-рядко срещаните. Това се вижда и в примера, даден по-долу.
Нека имаме низа "ABRACADABRA". Честотната таблица за низа е:
| Символ: | Брой срещания: |
|---|---|
| A | 5 |
| B | 2 |
| C | 1 |
| D | 1 |
| R | 2 |
Строим дървото по следния начин:

На всеки клон от дървото съпоставяме двоична цифра 0 или 1: 0 за ляв клон, 1 за десен клон. Така на всеки път от корена до някое листо отговаря двоичен низ. Тъй като всяко листо беше символ от низа, можем да съпоставим на всеки символ двоичната последователност, която съответства на пътя от корена до листото на символа. Тъй като най-често срещаните символи са най-близко до корена, на тях ще отговарят най-къси последователности. Обратно - на рядко срещаните символи съответстват дълги последователности.
Продължаваме примера отгоре. Дървото, отбелязано с 0 и 1 изглежда така:
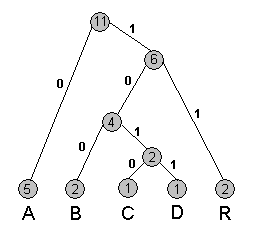
Таблицата за кодиране е:
| Символ: | Код: |
|---|---|
| A | 0 |
| B | 100 |
| C | 1010 |
| D | 1011 |
| R | 11 |
След като получим таблицата за кодиране, извършваме кодиране на низа - всеки символ заместваме с неговия код. Така получаваме последователност от 0 и 1. Ако разбием на блокове по 8 бита, можем да получим и изход от байтове.
ABRACADABRA --> 0 100 11 0 1010 0 1011 0 100 11 0 --> 01001101010010110100110 01001101010010110100110 --> 01001101 01001011 0100110 --> 77 75 38
От 11 символа (байта) = 8*11 бита = 88 бита получихме 23 бита компресирана информация - около 26% от оригиналния обем. Получихме четири пъти по-малко описание на "ABRACADABRA".
Разкомпресирането на данните става лесно при условие, че имаме дървото на Хъфман. Вървим едновременно по двоичния низ и по дървото, като всеки път като срещнем 0 завиваме наляво, а при 1 - надясно. Когато стигнем до листо, записваме съответния символ и рестартираме от корена. Така стъпка по стъпка получаваме първоначалния низ.
01001101010010110100110 --> 0 100 11 0 1010 0 1011 0 100 11 0 --> A B R A C A D A B R A
Да се напише програма, която въвежда низ от клавиатурата (или от файл), построява честотна таблица и дървото на Хъфман и извежда двоичната последователност, която кодира оригиналния низ. Да се пресметне степента на компресия (отношението на броя на битовете на компресираната и декомпресираната последователност - считаме, че всеки символ се кодира с един байт). По дървото на Хъфман да се възстанови оригиналният низ.
Допълнителни задачи:
Описаният алгоритъм е един от най-простите алгоритми за компресиране. Това е универсален алгоритъм без загуба на информация за кодиране с променлива дължина. За декодиране е необходимо да се пази допълнителна структура - в случая честотна таблица или дърво на Хъфман. За сравнение има алгоритми (LZ77, LZ78), които не се нуждаят от допълнителна структура, а строят такава динамично по време на компресия и декомпресия въз основа на самата информация. На алгоритъма на Хъфман има направени много подобрения, които го усложняват, но подобряват степента на компресиране.
Задачата подготви: Трифон Трифонов