- Един връх трябва да има не повече от един родител - иначе ще получим повече от едно входни ребра за някой от върховете.
- Трябва да има единствен връх, който няма родители - иначе ще получим гора.
- Графът трябва да е ацикличен.
- **Всеки връх трябва да има не повече от два наследника - в противен случай ще получим не двоично, а напълно произволно дърво.
"Правилен критерий е: графът да е ацикличен, всички възли да имат поне един родител и да има точно един възел без родители" - даже това е малко грешно.
Ако ти е направило впечатление, условието е "Да се напише функция, която проверява дали даден ориентиран граф е дърво."
Така че критериите са си напълно в нормата. Вече в isBinTree се прави допълнителната проверка дали е точно двоично дърво, а не някое произволно.
Разбира се, никой не е казал, че не можеш да го напишеш в една функция, която едновременно проверява дали графът е дърво и ако да, дали е двоично.
Въпрос на личен избор.
Така че критериите са си напълно в нормата. Вече в isBinTree се прави допълнителната проверка дали е точно двоично дърво, а не някое произволно.
Разбира се, никой не е казал, че не можеш да го напишеш в една функция, която едновременно проверява дали графът е дърво и ако да, дали е двоично.
Въпрос на личен избор.
Цитирам условието:
"Да се напише функция
Все пак, в случая не това е водещото.
В критериите, които бяха качени, дори без този, който добавих, ако ги прочетеш много внимателно, ще откриеш, че е допусната малка грешка, отнасяща се до броя на родителите - просто не може дърво да има връх, който има повече от един родител.
"Да се напише функция
BinTree<int> toBinTree (IntGraph& g)която проверява дали един ориентиран граф може да се разглежда като двоично дърво и ако може, построява това дърво. "
Все пак, в случая не това е водещото.
В критериите, които бяха качени, дори без този, който добавих, ако ги прочетеш много внимателно, ще откриеш, че е допусната малка грешка, отнасяща се до броя на родителите - просто не може дърво да има връх, който има повече от един родител.
Ох, защо се захванах. Хайде и аз да цитирам:
Графи
Та, ако още не е ясно, критикуваш условията на допълнителните задачки, които ще ти помогнат да решиш самото домашно. И които са писани на упражнения, явно не си присъствала на тях. Не знам за теб, но според мен е по-лесно да се направи проверка дали дадено дърво е двоично, след като вече сме проверили, че наистина става дума за дърво. Освен това никъде не пише, че трябва някой от върховете да има повече от два родителя, точно обратното. Прочети си всичко внимателно и ще разбереш, че съм права.
Графи
- Да се напише функция, която проверява дали граф, зададен със списък от насленици е ориентиран или неориентиран, т.е. дали за всяка дъга имаме обратна дъга.
- Да се напише функция, която проверява дали даден ориентиран граф е дърво. Примери за непълни критерии:
- графът да е ацикличен (може да имаме 1 -> 2, 2 -> 3, 1-> 3)
- всички възли да имат поне един родител (може да имаме цикъл)
- всички възли да имат поне един родител и да има възел без родители (може да имаме гора)
- всички възли да имат поне един родител и да има точно един възел без родители (може да имаме 1 -> 2, 3 -> 4, 4 -> 3)
Та, ако още не е ясно, критикуваш условията на допълнителните задачки, които ще ти помогнат да решиш самото домашно. И които са писани на упражнения, явно не си присъствала на тях. Не знам за теб, но според мен е по-лесно да се направи проверка дали дадено дърво е двоично, след като вече сме проверили, че наистина става дума за дърво. Освен това никъде не пише, че трябва някой от върховете да има повече от два родителя, точно обратното. Прочети си всичко внимателно и ще разбереш, че съм права.
Според теб в едно дърво може ли да има връх, с повече от един родител?
Критикувам едно единствено условие - това за броя на родителите.
"всички възли да имат поне един родител" <=> "един или повече"
Не пише, че трябва, но не пише и точно обратното.
Чета внимателно и затова обръщам внимание на тези неща.
И понеже това вече се превръща в абсолютно безмислен спор, ще спра с коментарите.
A little hint:
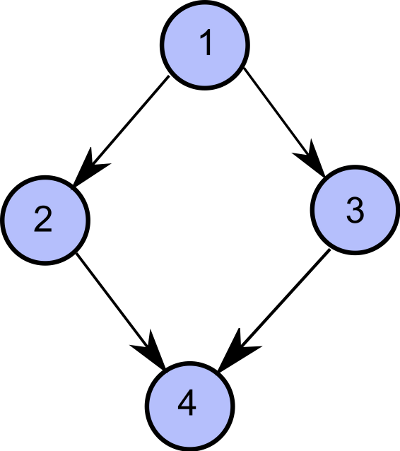
1->2;
1->3;
2->4;
3->4;
Няма цикли. Има точно един връх без родители. Всеки друг връх има поне един родител.
Enjoy! (:
Критикувам едно единствено условие - това за броя на родителите.
"всички възли да имат поне един родител" <=> "един или повече"
Не пише, че трябва, но не пише и точно обратното.
Чета внимателно и затова обръщам внимание на тези неща.
И понеже това вече се превръща в абсолютно безмислен спор, ще спра с коментарите.
A little hint:
1->2;
1->3;
2->4;
3->4;
Няма цикли. Има точно един връх без родители. Всеки друг връх има поне един родител.
Enjoy! (:
Ясно ми е какво критикуваш, също така ми е ясно, че в момента се хващаш за една дума. Първият ми отговор беше относно 4**, за да обясня, че проверката за броя наследници нарочно е пропусната във въпросното условие. А ти задълба в друга посока.
Аз приключвам въпроса.
Аз приключвам въпроса.
Права си, думата "поне" трябва да се замени с "най-много" в целия текст. Благодаря за поправката, нанесох я в текста.