Често срещани грешки в домашните
От проверените досега домашни (около 2/3), следните грешки са най-често срещани.
1) В задача 1.4 не е обосновано адекватно рекурентното уравнение. Повечето работи съдържат коректно уравнение. Намерено е в Интернет, чудесно. Това го казвам без ирония. Умението да се търси информация е важно. Но уравнението трябва да се обоснове.
А пропо, следната обосновка не е валидна:
Sn = Sn-1 + Sn-1 + <ощенещо>
като първото Sn-1 е заради възможността само (c,an) да е в дървото, второто е заради възможността (an, an-1) да е в дървото, а <ощенещо> отразява възможността и (c,an), и (an, an-1) да са в дървото. Това трето събираемо, казва обосновката, е Sn-1 - Sn-2, защото от множеството ПД на Dn-1 махаме тези, които съдържат (c,an-1).
Тази обосновка е нагласена да дава коректен израз, но е невалидна. При положение, че не знаем точно колко са ПД на Dn, няма как да знаем, че ПД на Dn-1, несъдържащи (c,an-1) са Sn-1 - Sn-2. И те наистина не са толкова. Цикъл може да се получи не само чрез реброто (c,an-1), а и чрез някое (c, ai) за i < n-1. Прилагам снимка на дъската в кабинета ми; дано е ясно от нея.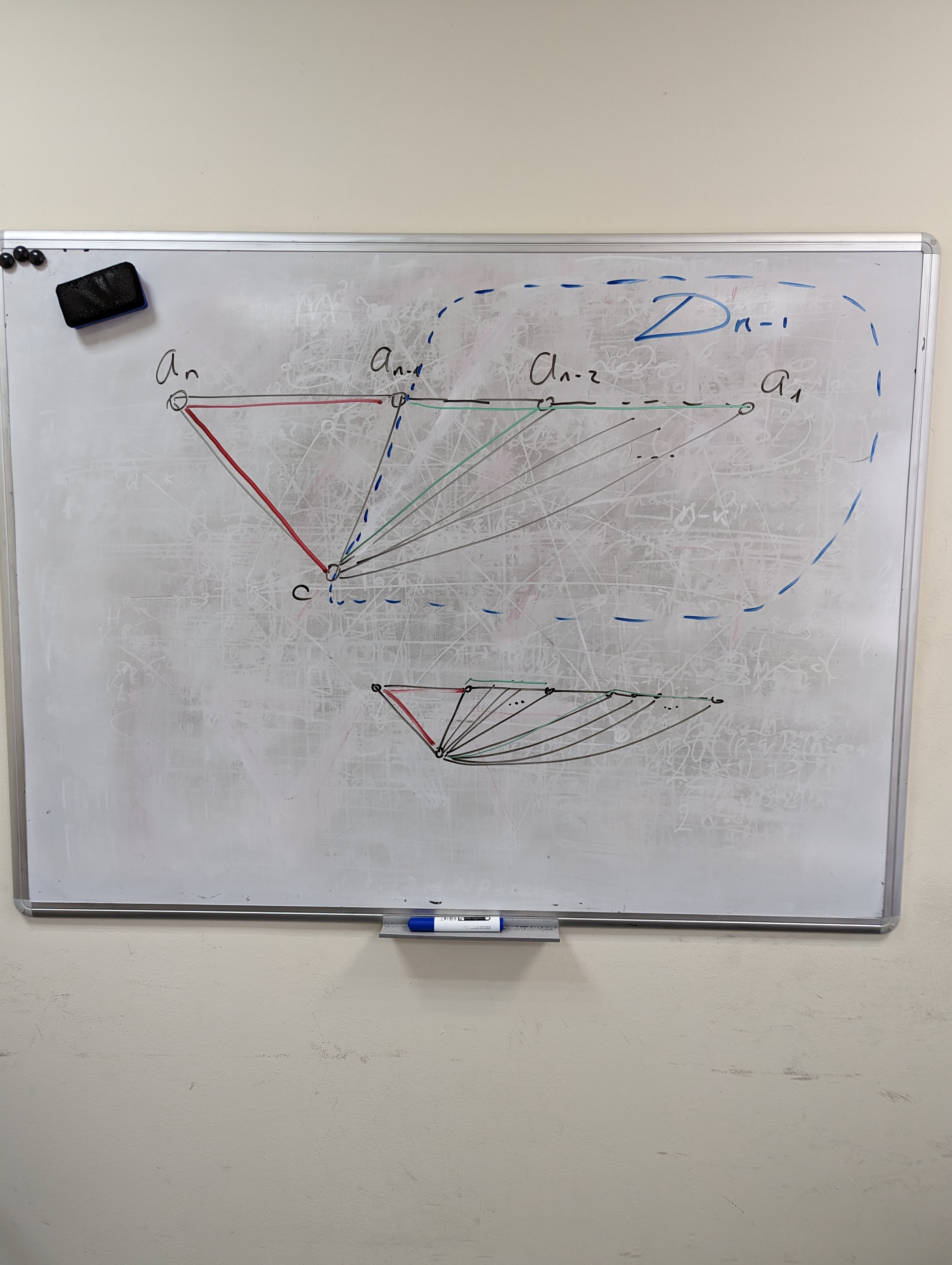
2) В зад 2 повечето са намерили графа на Mycielski като контрапример
https://mathworld.wolfram.com/MycielskiGraph.html
Чудесно, важно умение е да се търси информация онлайн. Но трябва валидна обосновка. При кратко търсене не намерих сайт, който да обяснява защо \chi(G) > 3 за този граф. Невалидна е следната обосновка (горе-долу в този дух): първият връх от външния цикъл трябва да е в някакъв цвят, БОО нека е червен, съседът му е, да кажем, зелен (дотук е ОК), и после се описва някакво оцветяване, при което се стига до противоречие. Невалидността е в това, че АКО по този начин не става, това не означава непременно, че по никой друг начин не става. Трябва да има аргументация, че разгледаният начин е без ограничение на общността. Без такава аргументация, би трябвало да се разгледат с backtracking кой знае колко възможни начала на 3-оцветяване, за да се стигне до противоречие по всеки път от корена до листо (на дървото на backtracking-а).
ПП валидната обосновка за графа на M, която аз виждам, е да се съобрази, че бройките на цветовете в-у външния цикъл трябва да са 1,2,2 (ако работим при допускането, че \chi(G) = 3). Това го вземам за очевидно -- не може да са 1,1,3, а друга възможна сума на 5 от три цели положит. събираеми няма. Тогава разглеждаме върха от външния цикъл, който е единствен в цвета си. Оттук решението следва много бързо, понеже другите два цвята трябва да се редуват, има само два начина за това, БОО разглеждаме само единият, и оттам изводът е директен. Но е БОО.